library(dplyr)
library(haven)
library(here)
library(tidyverse)
library(ggplot2)
library(ggrepel)
library(stargazer)
library(visreg)
library(kableExtra)
library(reshape2)
library(fBasics)
library(questionr)
library(ggmosaic)
library(pander)
library(DescTools)
library(conf)Central Limit Theory
Rata-rata sampel acak dari suatu populasi memiliki nilai yang diharapkan \(\mu\) dan standar deviasi \(\frac {\sigma}{\sqrt(n)}\) dengan \(\mu\) dan \(\sigma\) adalah parameter populasi.
n <- 25; curve(dnorm(x, mean=0, sd=1/sqrt(n)), -3, 3,
xlab="x", ylab="Densities of sample mean", bty="l")
n <- 5; curve(dnorm(x, mean=0, sd=1/sqrt(n)), add=TRUE)
n <- 1; curve(dnorm(x, mean=0, sd=1/sqrt(n)), add=TRUE)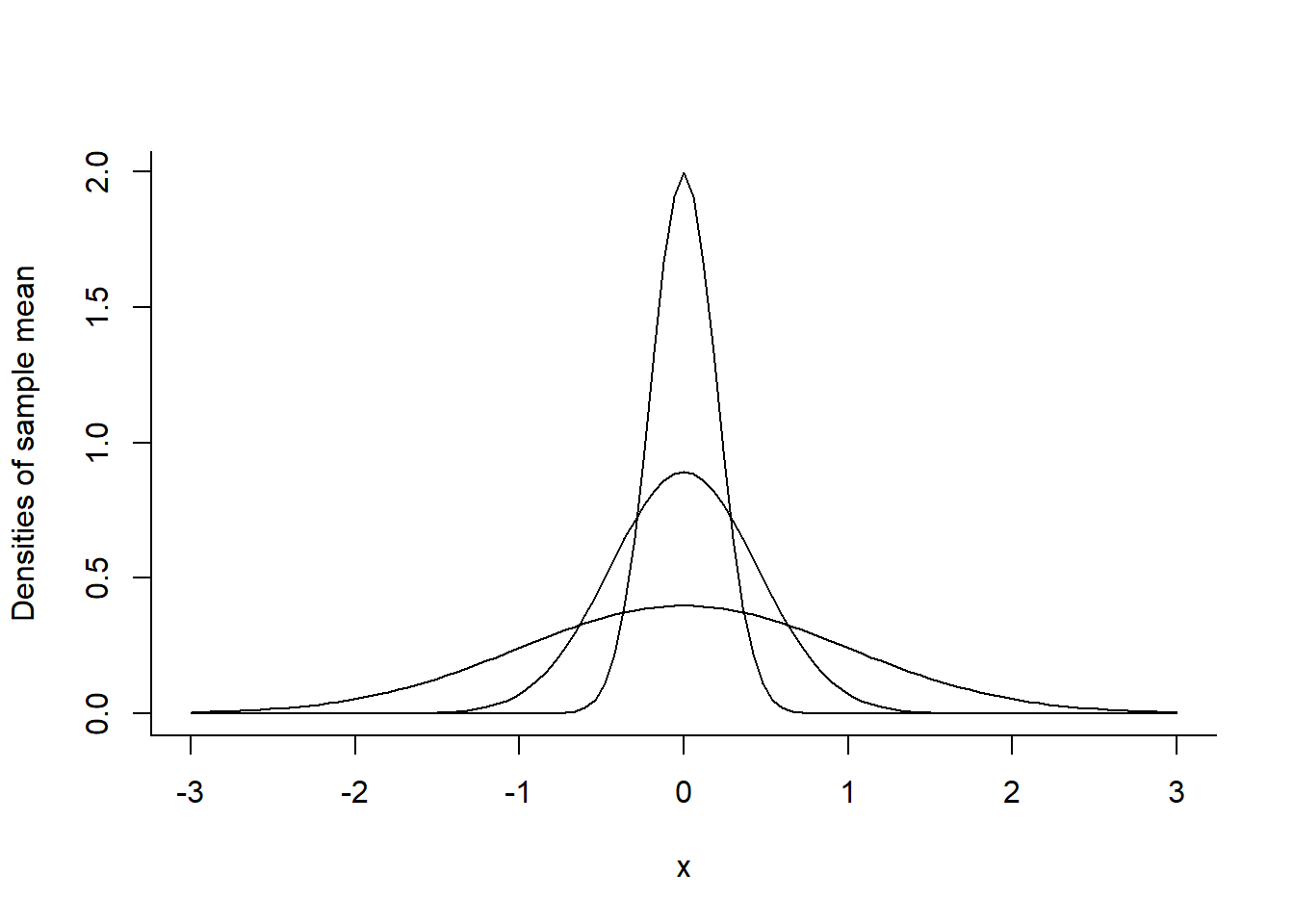
Normal parent population
Ketika sampel \(X_1\), \(X_2\), \(X_3\),…, \(X_n\) diperoleh dari populasi Normal (\(\mu\), \(\sigma\)), \(\bar {X}\) berdistribusi normal. Gambar diatas menunjukkan kepadatan populasi dan distribusi sampel dari \(\bar {X}\) untuk n = 5 dan n = 25 ketika \(\mu = 0\) dan \(\sigma = 1\).
Dari gambar terlihat seiring betambahnya n, \(\bar {X}\) semakin kecil. Jika ukuran sampel bertamah 4 kali lipat, maka standar deviasinya \(\frac{1}{2}\) dari populasi.
Kepadatan terkonsentrasi pada mean. Semakin besar probablitas, nilai acak \(\bar {X}\) semakin dekat dengan mean. Hal ini dikenal dengan hukum bilangan besar (law of large numbers). Misalnya tinggi wanita dewasa berdistribusi normal dengan rata-rata 65 inci dan standar deviasi 2,2 inci. Rata-rata 20 wanita dewasa dipilih secara acak dan diperoleh rata-rata yang sama tetapi standar deviasi lebih besar \(\frac {1}{5}\) kali. Perbandingan probabilitas rata-rata antara sampel 64 dan 65 dengan individu adalah:
mu <- 65; sigma <- 2.2; n <- 20
pnorm(65, mu, sigma/sqrt(n)) - pnorm(64, mu, sigma/sqrt(n)) # rata-rata[1] 0.4789631pnorm(65, mu, sigma) - pnorm(64, mu, sigma) # individu[1] 0.1752819Non normal parent population
Central limit theory menyatakan bahwa setiap populasi induk (parent population) dengan rata-rata \(\mu\) dan standar deviasi \(\sigma\), distribusi sampel dari \(\bar{X}\) untuj jumlah populasi (n) yang besar adalah
\[ P{\frac{\bar{X}-\mu}{\sigma/\sqrt{n}}\leq b} \approx P(Z\leq b) \]
Contoh:
Waktu yang dibutuhkan untuk mencuci mobil bervariasi. Checker mrmiliki rata-rata historis waktu mencuci satu jam per mobil, dengan standar deviasi satu jam. Jika terdapat 30 mobil yang dicuci, berapa probabilitas rata-rata mencuci mobil 0.9 jam atau kurang? Kami berasumsi bahwa setiap waktu mencuci memiliki populasi induk yang tidak ditentukan dengan \(\mu=1\) dan \(\sigma=1\), dan urutan waktu pencucian mobil acak, serta n cukup besar sehingga \(\bar{X}\) kira-kira berdistribusi Normal(\(\mu,\sigma/\sqrt{30}\)). Sehingga \(P(\bar{X}\leq0.9)\) adalah
pnorm(0.9, mean=1, sd = 1/sqrt(20))[1] 0.3273604Tredapat konsekuensi lain dari teorema limit pusat. Misalnya jika kami mengganti \(\sigma\) dengan standar deviasi sampel \(s\) dan \(\bar{X}\) distandarisasi maka
\[ P{\frac{\bar{X}-\mu}{s/\sqrt{n}}\leq b} \approx P(Z\leq b) \]